about
The Machine Learning Research Lab focuses on
fundamental machine learning research for probabilistic inference,
time series modelling, efficient exploration, and control.
Our work starts from probability theory, through neural networks, to applications inside and outside our lab.
This website is to inform you about our work through publications, blog posts, and other public output.
Disclaimer: The views, thoughts, and opinions expressed on this website belong solely to the individual authors/contributors and do not necessarily reflect the official policy or position of Volkswagen Group. The content provided is for informational purposes only and is not intended as legal, financial, or professional advice. Volkswagen Group makes no representations as to the accuracy, completeness, suitability, or validity of any information on this site and will not be liable for any errors, omissions, or delays in this information or any losses, injuries, or damages arising from its display or use. All information is provided on an as-is basis. It is the reader's responsibility to verify their own facts.
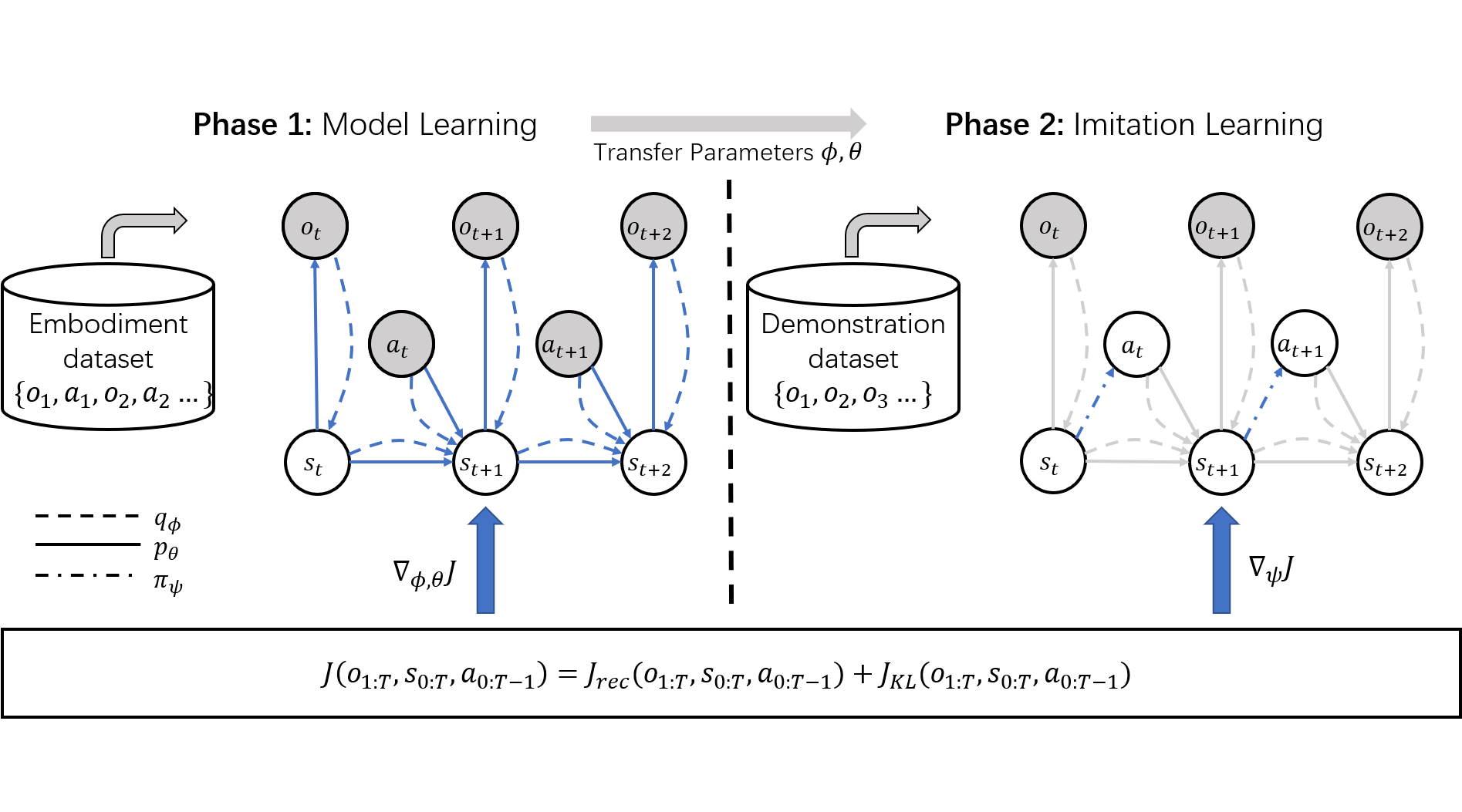
Action Inference by Maximising Evidence
Spatial World Models
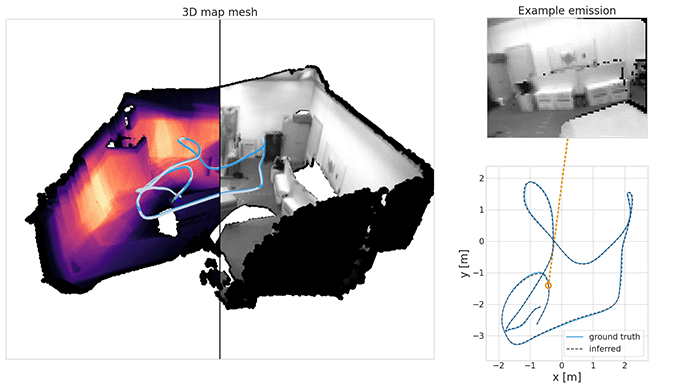
Spatial World Models

Latent Matters
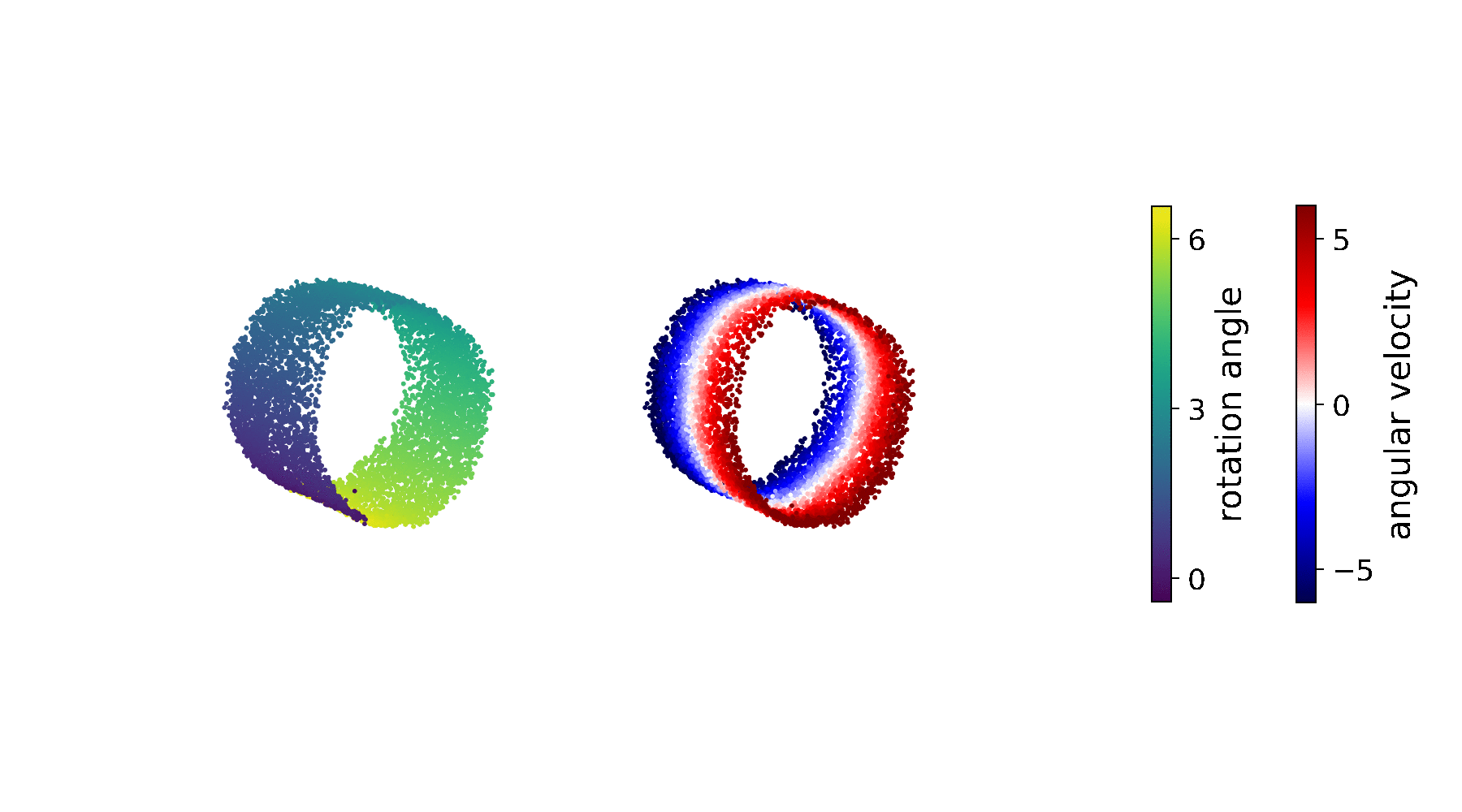
10toGO: Virtual thinkathon for Sustainable Development Goals

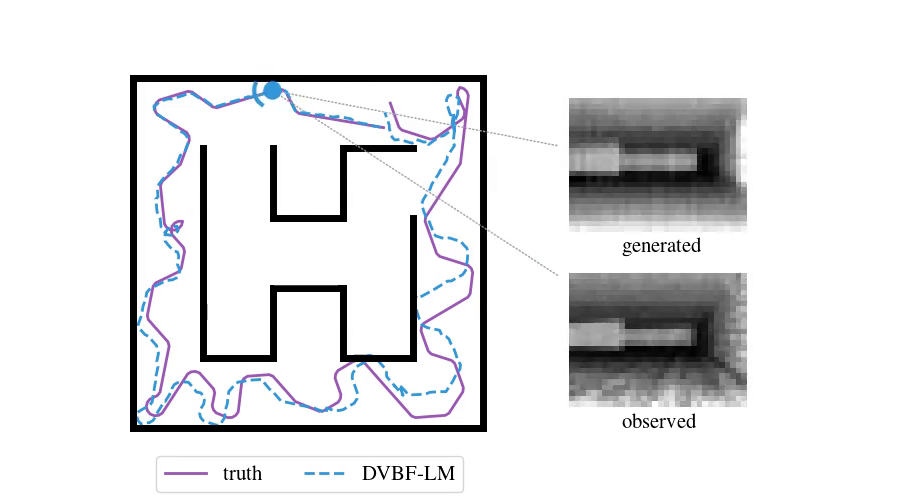
Variational State-Space Models for Localisation and Dense 3D Mapping in 6 DoF

Less Suboptimal Learning and Control in Variational POMPDs
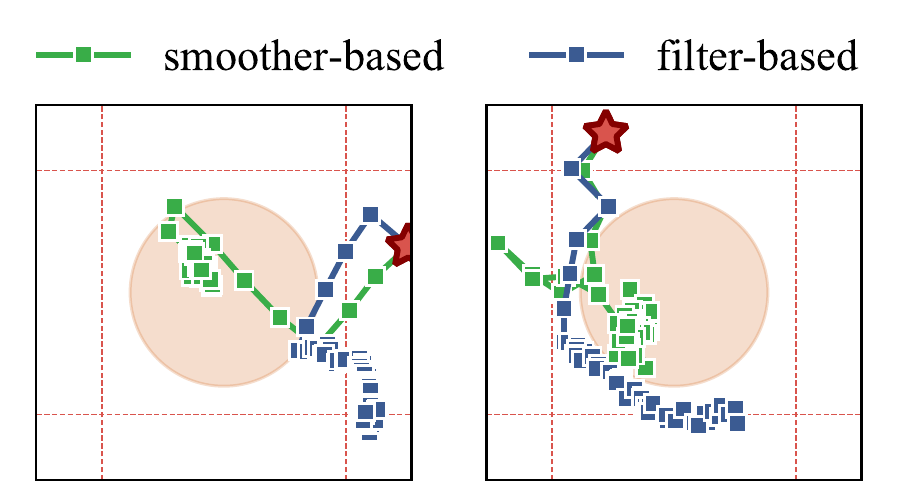
A Tale of Gaps
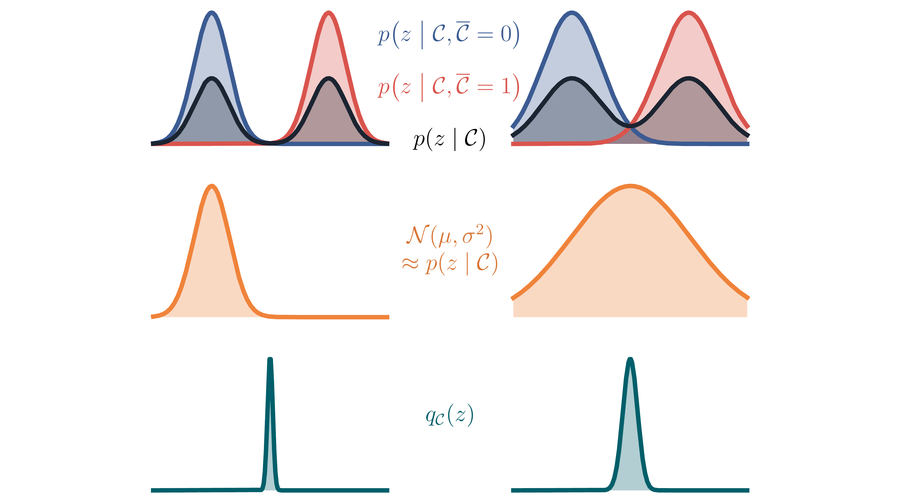
Continual Learning with Bayesian Neural Networks for Non-Stationary Data
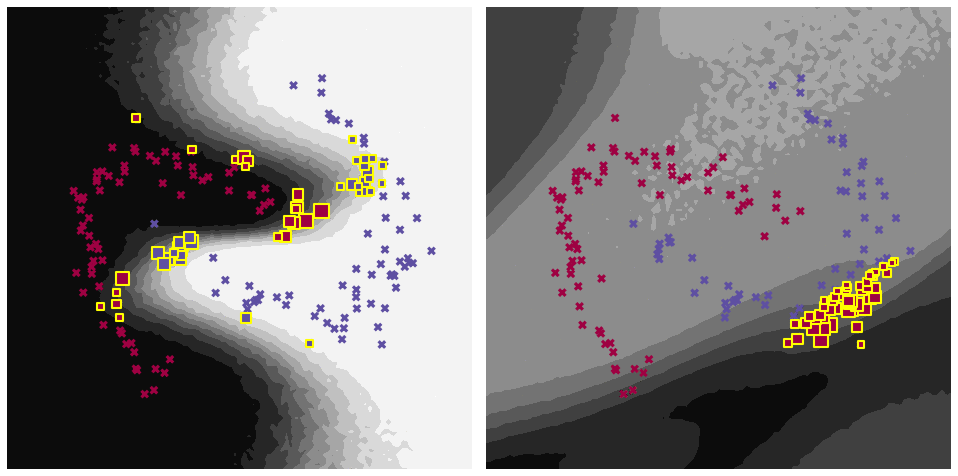
Estimating Fingertip Forces, Torques, and Object Curvatures from Fingernail Images

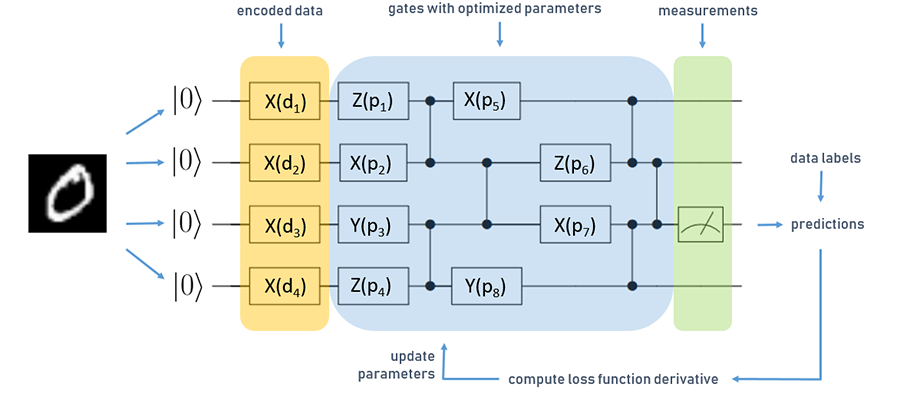
Layerwise learning for quantum neural networks
Learning to Fly

Learning Flat Manifold of VAEs
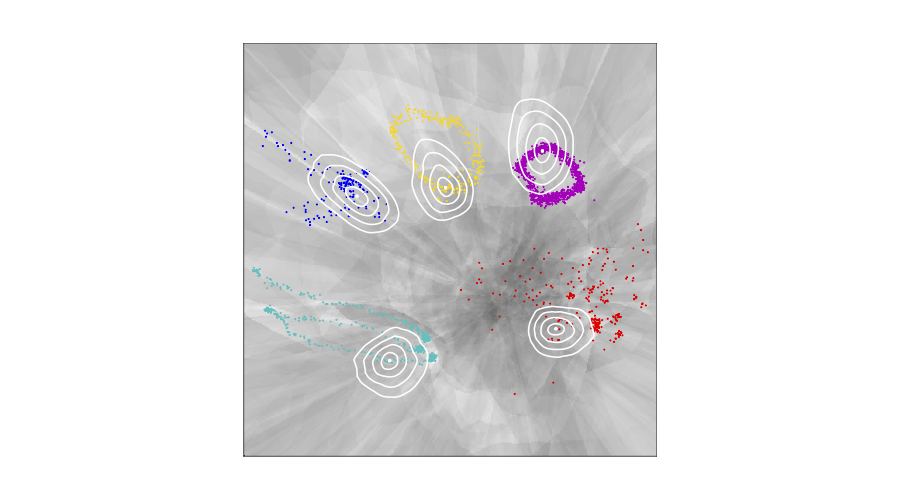
Approximate Bayesian inference in spatial environments
Learning Hierarchical Priors in VAEs

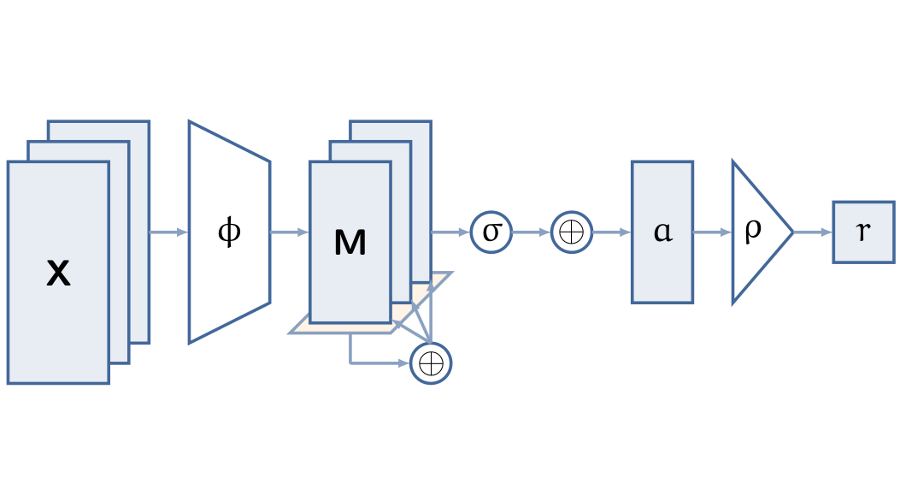
How to Learn Functions on Sets with Neural Networks
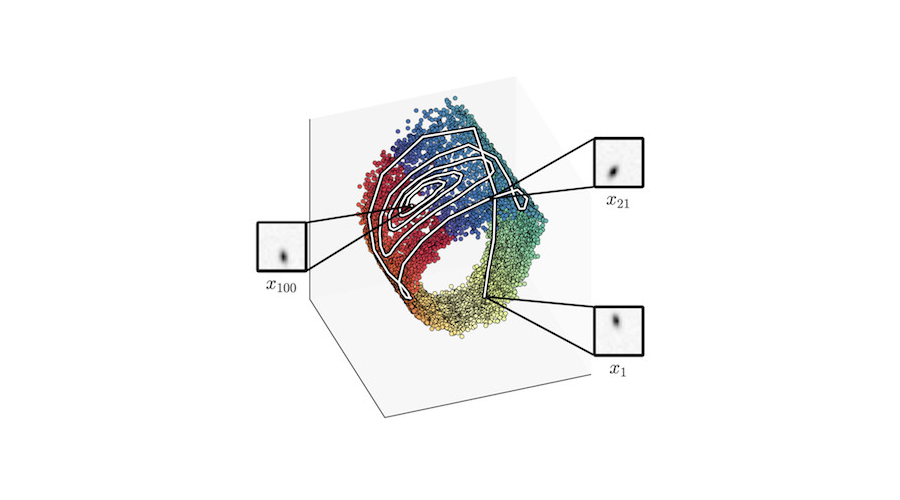
Approximate Geodesics for Deep Generative Models

Network Architecture Optimisation

Deep Variational Bayes Filter
About